Rewrite Triple Integrals Using Cylindrical Coordinates YouTube

Triple Integral and Volume Using Cylindrical Coordinates YouTube

Calculus 3 tutorial video that explains triple integrals in cylindrical coordinates: how to read and think in cylindrical coordinates, what the integrals mea.

Triple Integrals Using Cylindrical Coordinates 2 Vector Calculus

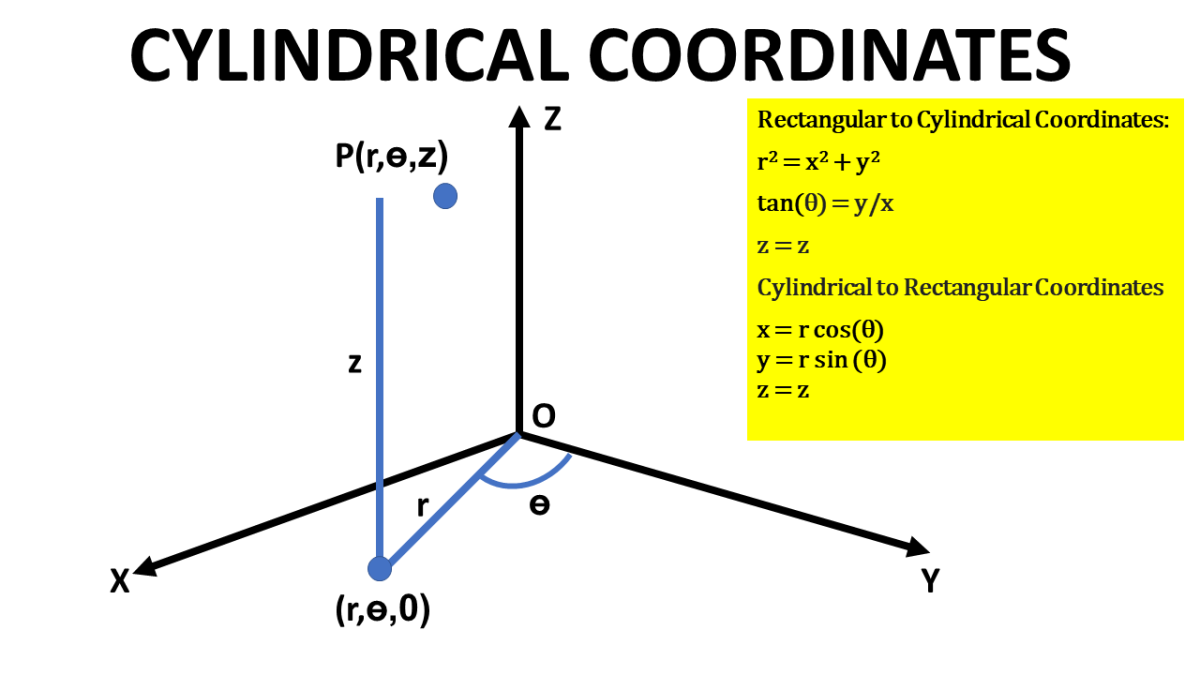
Definition. Cylindrical coordinates represent a point P in space by the ordered triple (r, θ, z) where r and θ are the polar coordinates for the vertical projection of P onto the xy-plane. z is the rectangular vertical coordinate of P . z P (r, θ, z) b b y x

Video3234 Triple Integrals in Cylindrical Coordinates Practice

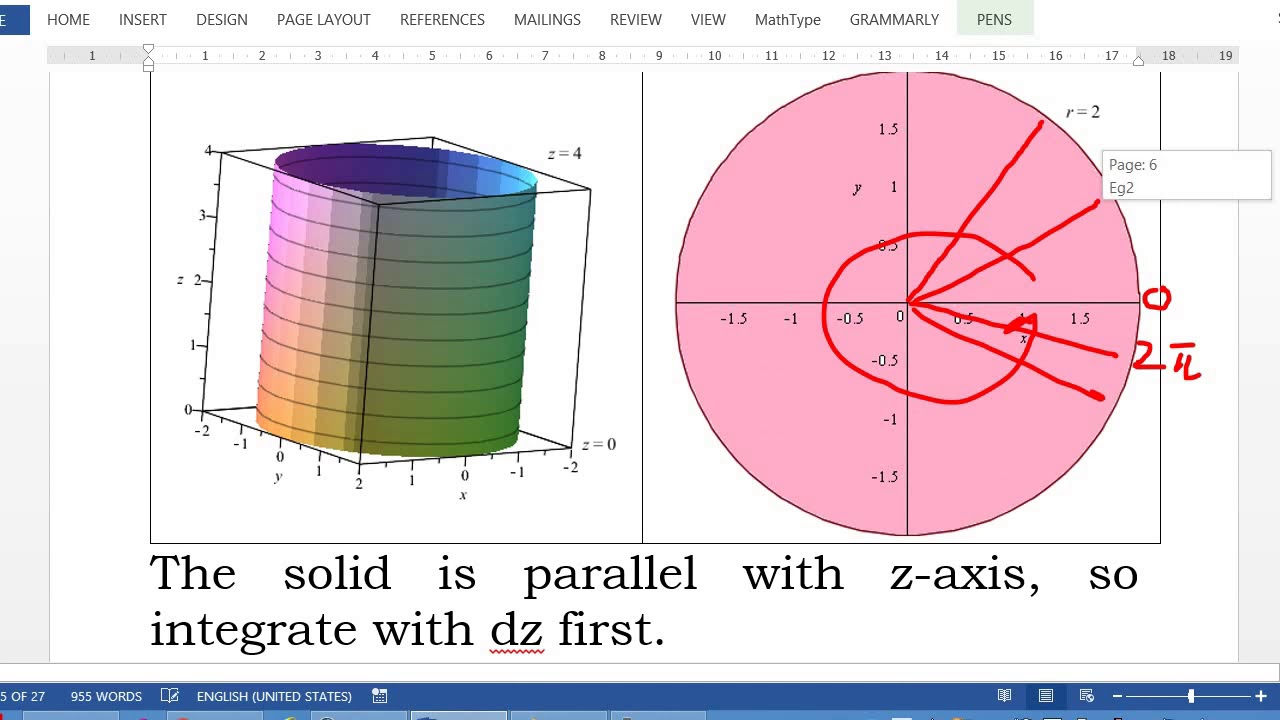
Integration in Cylindrical Coordinates: To perform triple integrals in cylindrical coordinates, and to switch from cylindrical coordinates to Cartesian coordinates, you use: x= rcos ; y= rsin ; z= z; and dV = dzdA= rdzdrd : Example 3.6.1. Find the volume of the solid region Swhich is above the half-cone

Rewrite Triple Integrals Using Cylindrical Coordinates YouTube

By adding the z-axis, the circle has a height of z, which gives it the shape of a cylinder, hence the name cylindrical coordinates. As seen in Double Integrals in Polar Form, when converting a double integral from Cartesian to polar coordinates, the \(dA\) term, \(dx\,dy\) in Cartesian gets converted to its polar equivilent.

Triple Integral by cylindrical coordinates YouTube

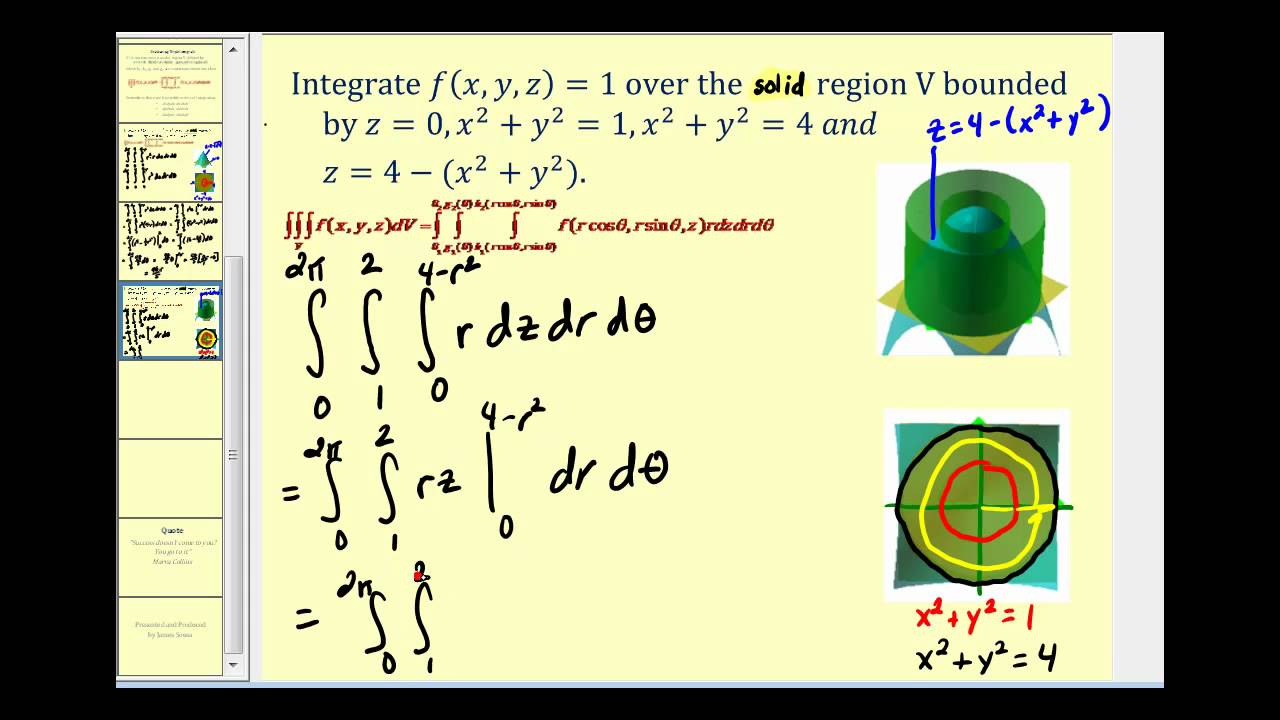
To change a triple integral into cylindrical coordinates, we'll need to convert the limits of integration, the function itself, and dV from rectangular coordinates into cylindrical coordinates. The variable z remains, but x will change to rcos (theta), and y will change to rsin (theta). dV will convert to r dz dr d (theta).

Cylindrical Coordinates Rectangular to Cylindrical Coordinates

Integration in cylindrical coordinates is a simple extension of polar coordinates from two to three dimensions. This coordinate system works best when integrating cylinders or cylindrical-like objects. As with spherical coordinates, cylindrical coordinates benefit from lack of dependency between the variables, which allows for easy factoring. Steps

Calc III Triple Integrals in Cylindrical Coordinates example 3/6 YouTube

1. Evaluate the triple integral in cylindrical coordinates: f(x; y; z) = sin(x2 + y2), W is the solid cylinder with height 4 with base of radius 1 centered on the z-axis at z = 1. Spherical Coordinates The spherical coordinates of a point (x; y; z) in 3 R are the analog of polar coordinates in R 2.

SOLUTION 6 triple integrals in cylindrical and spherical coordinates

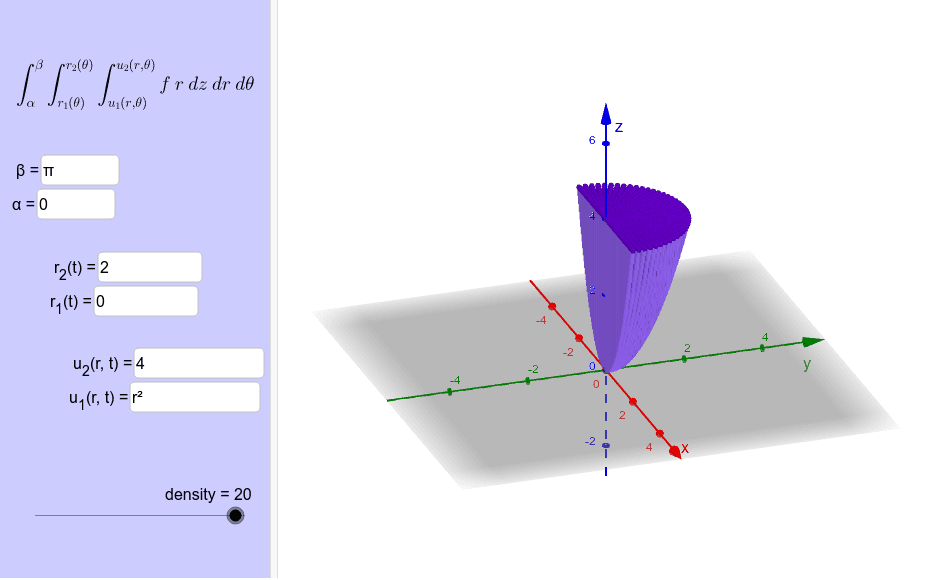
In terms of cylindrical coordinates a triple integral is, ∭ E f (x,y,z) dV = ∫ β α ∫ h2(θ) h1(θ) ∫ u2(rcosθ,rsinθ) u1(rcosθ,rsinθ) rf (rcosθ,rsinθ,z) dzdrdθ ∭ E f ( x, y, z) d V = ∫ α β ∫ h 1 ( θ) h 2 ( θ) ∫ u 1 ( r cos θ, r sin θ) u 2 ( r cos θ, r sin θ) r f ( r cos θ, r sin θ, z) d z d r d θ

Triple Integrals Using Cylindrical Coordinates YouTube

Now we can use 3.6.3 to handle a variant of Example 3.5.1 in which the density is invariant under rotations around the z z -axis. Cylindrical coordinates are tuned to provide easier integrals to evaluate when the integrand is invariant under rotations about the z z -axis, or when the domain of integration is cylindrical.

Lesson 2 Triple Integrals in Cylindrical Coordinates (Calculus 3

3. Evaluate ∭ E zdV ∭ E z d V where E E is the region between the two planes x+y +z = 2 x + y + z = 2 and x = 0 x = 0 and inside the cylinder y2+z2 = 1 y 2 + z 2 = 1. Show All Steps Hide All Steps. Start Solution.

Converting triple integrals to cylindrical coordinates (KristaKingMath

We are integrating \(z\) first in the integral set up to use Cartesian coordinates and so we'll integrate that first in the integral set up to use cylindrical coordinates as well. It is easy to convert the \(z\) limits to cylindrical coordinates as follows. \[{r^2} - 11 \le z \le 9 - 3{r^2}\] Show Step 3

Triple Integral in Cylindrical Coordinates Visualizer GeoGebra

Answer. Example : Finding a Volume with Triple Integrals in Two Ways. Let E be the region bounded below by the -plane, above by the sphere , and on the sides by the cylinder. (Figure 15.5.5). Set up a triple integral in cylindrical coordinates to find the volume of the region using the following orders of.

4c. Volume of a cone as a triple integral in cylindrical coordinates

Figure 15.7.3: Setting up a triple integral in cylindrical coordinates over a cylindrical region. Solution. First, identify that the equation for the sphere is r2 + z2 = 16. We can see that the limits for z are from 0 to z = √16 − r2. Then the limits for r are from 0 to r = 2sinθ.

Video3230 Triple Integrals in Cylindrical Coordinates Example YouTube

0,0. Δr. rΔθ. Figure 15.2.1. A cylindrical coordinates "grid''. Example 15.2.1 Find the volume under z = √4 − r2 above the quarter circle bounded by the two axes and the circle x2 + y2 = 4 in the first quadrant. In terms of r and θ, this region is described by the restrictions 0 ≤ r ≤ 2 and 0 ≤ θ ≤ π / 2, so we have ∫π / 2.

13.7 Integration in Cylindrical Coordinates, Part 2 YouTube

With cylindrical coordinates (r, θ, z), by r = c, θ = α, and z = m, where c, α, and m are constants, we mean an unbounded vertical cylinder with the z -axis as its radial axis; a plane making a constant angle α with the xy -plane; and an unbounded horizontal plane parallel to the xy -plane, respectively.

7 Center of mass, Triple integrals, Cylindrical coordinates YouTube

Using cylindrical coordinates can greatly simplify a triple integral when the region you are integrating over has some kind of rotational symmetry about the z -axis. The one rule When performing double integrals in polar coordinates, the one key thing to remember is how to expand the tiny unit of area d A in terms of d r and d θ