Hockey Stick Identity Brilliant Math & Science Wiki

Art of Problem Solving Hockey Stick Identity Part 1 YouTube
1. Prove the hockeystick identity X r n = n + r + 1 + k k=0 k r when n; r 0 by using a combinatorial argument. (You want to choose r objects. For each k: choose the rst r k in a row, skip one, then how many choices do you have for the remaining objects?)

Art of Problem Solving Hockey Stick Identity Part 5 YouTube
In combinatorial mathematics, the hockey-stick identity, [1] Christmas stocking identity, [2] boomerang identity, Fermat's identity or Chu's Theorem, [3] states that if n ≥ r ≥ 0 are integers, then. ( r r) + ( r + 1 r) + ( r + 2 r) + ⋯ + ( n r) = ( n + 1 r + 1). The name stems from the graphical representation of the identity on Pascal's.

Hockey Stick in Pascal’s Triangle Combinatorics Math Olympiad
Combinatorial identity Contents 1 Pascal's Identity 1.1 Proof 1.2 Alternate Proofs 2 Vandermonde's Identity 2.1 Video Proof 2.2 Combinatorial Proof 2.3 Algebraic proof 3 Hockey-Stick Identity 3.1 Proof 4 Another Identity 4.1 Hat Proof 4.2 Proof 2 5 Even Odd Identity 6 Examples 7 See also Pascal's Identity Pascal's Identity states that
[Solved] Another Hockey Stick Identity 9to5Science
example 5 Use combinatorial reasoning to establish the Hockey Stick Identity: The right hand side counts the number of ways to form a committee of people from a group of people. To establish this identity we will double count this by assigning each of the people a unique integer from to and then partitioning the committees according to the.

Hockey stick identity How does it work if it starts at the left and
Use the Hockey Stick Identity in the form (This is best proven by a combinatorial argument that coincidentally pertains to the problem: count two ways the number of subsets of the first numbers with elements whose least element is , for .) Solution Solution 1 Let be the desired mean.

History Of Hockey Sticks [2022 InDepth Guide]
We think of picking a 3 person committee from a group of 6 as first choosing 2 from either the first 2, 3, 4, or 5 members to "arrive" at a meeting, and then.

Hockey Stick Size Guide With Sizing Chart Net World Sports
Another Hockey Stick Identity Asked 7 years, 7 months ago Modified 7 years, 7 months ago Viewed 1k times 4 I know this question has been asked before and has been answered here and here. I have a slightly different formulation of the Hockey Stick Identity and would like some help with a combinatorial argument to prove it.

Art of Problem Solving Hockey Stick Identity Part 2 YouTube
Hockey-stick identity - Wikipedia Hockey-stick identity Pascal's triangle, rows 0 through 7. The hockey stick identity confirms, for example: for n =6, r =2: 1+3+6+10+15=35.

MathType on Twitter "This identity is known as the Hockeystick
Hockey stick. For . This identity is known as the hockey-stick identity because, on Pascal's triangle, when the addends represented in the summation and the sum itself is highlighted, a hockey-stick shape is revealed. Proof. Inductive Proof. This identity can be proven by induction on . Base Case Let . . Inductive Step Suppose, for some , . Then .

prove Hockey Stick Identity
The hockey stick identity in combinatorics tells us that if we take the sum of the entries of a diagonal in Pascal's triangle, then the answer will be anothe.

Kookaburra Composite Hockey Stick Identity SKU KKBR_CIDTT www
We look at summation notation, and we are trying to solve 13.3. We think about forming a committee of 4 people, assuming that the members arrive not all at o.

What Does Flex on a Hockey Stick Mean KasonhasHorn
Let's discuss the Hockey Stick Identity from Combinatorics in Pascal's Triangle.https://www.cheenta.com/matholympiad/Visit https://www.cheenta.com/ for Advan.

Hockey Stick Identity Brilliant Math & Science Wiki
EDIT 01 : This identity is known as the hockey-stick identity because, on Pascal's triangle, when the addends represented in the summation and the sum itself are highlighted, a hockey-stick shape is revealed. combinatorics combinations binomial-coefficients faq Share Cite Follow edited Feb 7, 2023 at 6:25 Apass.Jack 13.3k 1 20 33
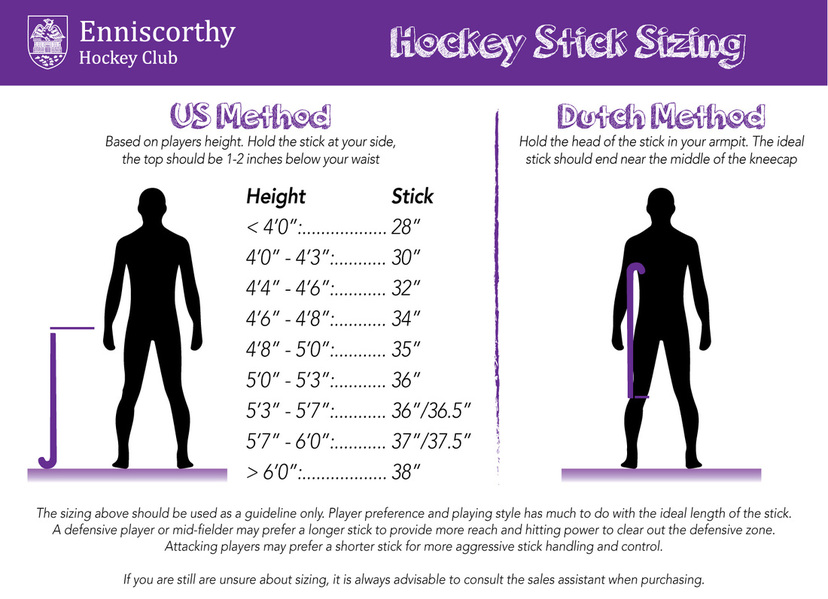
Selecting a Hockey Stick Enniscorthy Hockey Club
1 Properties 1.1 Binomial coefficients 1.2 Sum of previous values 1.3 Fibonacci numbers 1.4 Hockey-Stick Identity 1.5 Number Parity 1.5.1 Generalization 1.6 Patterns and Properties of the Pascal's Triangle 1.6.1 Rows 1.7 Diagonals 2 See Also Properties Binomial coefficients These are the first nine rows of Pascal's Triangle.

Hockey Stick Identity Brilliant Math & Science Wiki
This paper presents a simple bijection proof between a number and its combina-torial representation using mathematical induction and the Hockey-Stick identity of the Pascal's triangle. After stating the combinadic theorem and helping lemmas, section-2 proves the existence of combinatorial representation for a non-negative natural number.

FileHockey stick.svg Wikimedia Commons
In combinatorial mathematics, the hockey-stick identity, Christmas stocking identity, boomerang identity, Fermat's identity or Chu's Theorem, states that if are integers, then. Pascal's triangle, rows 0 through 7. The hockey stick identity confirms, for example: for n =6, r =2: 1+3+6+10+15=35. The name stems from the graphical representation of.